Plein ciel




MASSACRES Encouragés PAR LES SOLDATS ISRAELITES A SABRA ET SHATILA : comment qualifier cela et ne pas comprendre le raz le bol des résistants à l’ignominie fasciste d’extrême, extrême droite de la clique netanyaou and Co ?

PUNITION = APOCALYPSE DANS ISRAEL

Fin de Tel aviv

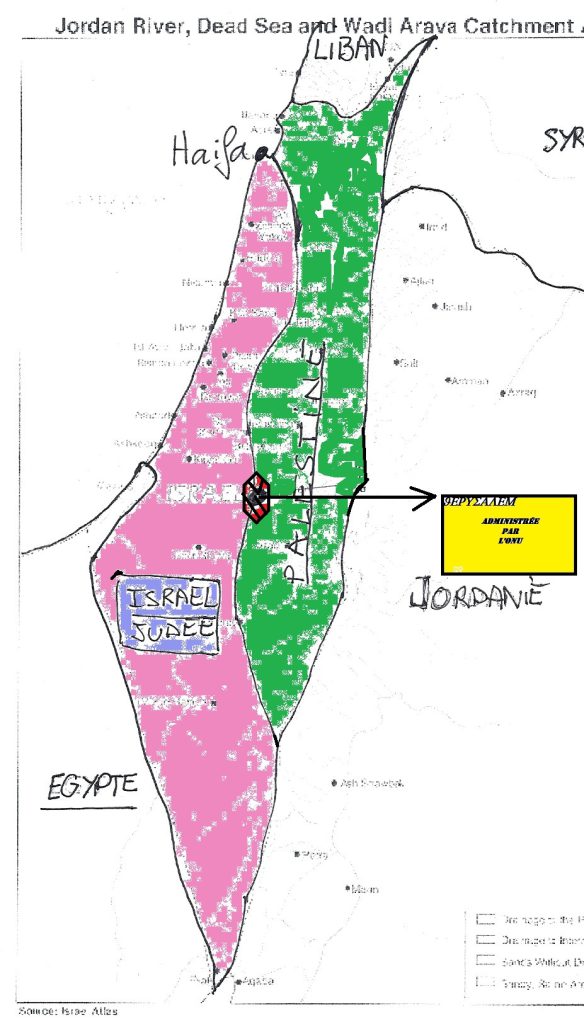
Les Palestinien(nes) sont les AUTOCHTONES cananéens ,
les israélites des envahisseurs cananéens ashkénazes qui se sont rassemblés à l’est de l’Europe et aux usa , les Juifs sont les séfarades d’Afrique du nord
J’avais un cheval
Dans un champ de ciel
Et je m’enfonçais
Dans le jour ardent.
Rien ne m’arrêtait
J’allais sans savoir,
C’était un navire
Plutôt qu’un cheval,
C’était un désir
Plutôt qu’un navire,
C’était un cheval
Comme on n’en voit pas,
Tête de coursier,
Robe de délire,
Un vent qui hennit
En se répandant.
Je montais toujours
Et faisais des signes :
« Suivez mon chemin,
Vous pouvez venir,
Mes meilleurs amis,
La route est sereine,
Le ciel est ouvert.
Mais qui parle ainsi ?
Je me perds de vue
Dans cette altitude,
Me distinguez vous,
Je suis celui qui
Parlait tout à l’heure,
Suis-je encor celui
Qui parle à présent,
Vous-mêmes, amis,
Êtes-vous les mêmes ?
L’un efface l’autre
Et change en montant. »
Jules Supervielle
La route est sereine,
Le ciel est ouvert
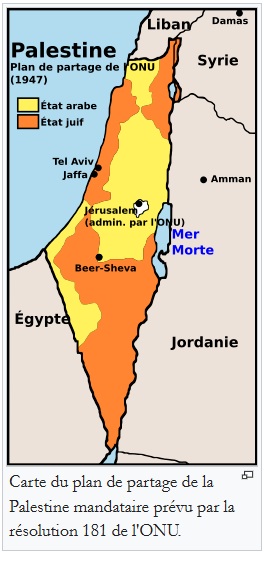
C’est pour quand et comment ?

Jeu avec l’I.A.



Raymond Abellio :
”La fin de l’ésotérisme”{Flam à Rions}
| … bla – bla – bla ]

C’est un ouvrage qui contient 5 exposés consacrés à l’ésotérisme, à ses doctrines d’abord, apparemment disparates, à ses applications ensuite, souvent réputées aventureuses, sinon fantaisistes ! UN SUJET IMMENSE qui concerne TOUTES LES CIVILISATIONS DEPUIS 60 SIèCLES, leurs MTHES, leurs CIVILISATIONS, leurs RELIGIONS, leurs PHILOSOPHIES, et aussi certaines de leurs activités + ou – SOUTERRAINES, telles que l’ALCHIMIE, la MAGIE, l’ASTROLOGIE, etc.
L’Auteur n’a pas voulu ici faire œuvre didactique et exhaustive, mais SEULEMENT DéGAGER QUELQUES FILS CONDUCTEURS ET SURTOUT EXPOSER UNE THèSE : à savoir, QU’EN CETTE FIN DE CYCLE HISTORIQUE, Nous entrons dans une Période de DéSOCCULTATION de la tradition CACHéE & que, dans cette désocultation, l’OCCIDENT doit tenir UN RÔLE éMINENT et faire CONFIANCE à SON EXIGENCE FONDAMENTALE de RATIONALITé, mais UNE RATIONALITé devenue TRANSCENDANTALE { Ce terme technique est d’abord utilisé en scolastique pour désigner les concepts qui, dépassant les catégories, sont si généraux qu’ils peuvent se convertir les uns dans les autres (comme « l’être est vrai » et « le vrai est »). L’un, le vrai, l’être… sont ainsi des transcendantaux } , moins expressive (?) qu’opérative ((1+1=3) est possible, tout dépend de quoi on parle)), – objective
( une casserole ça ne se mange pas) que TRANFIGURFATIVE
* Dans l’article ”TRANSFIGURER,, verbe trans.”
A. − Vieilli. Transformer totalement, métamorphoser. À ce moment, se produit une mue après laquelle l’embryon, devenu une véritable larve, est complètement transfiguré (E. Perrier, Zool., t. 1, 1893, p. 971).
B. − [L’obj. désigne une pers., un attribut de la pers.]
1.
A réaliser

a) [Le suj. désigne un inanimé] Transformer en donnant à une personne humaine, à son visage et à son expression un éclat inhabituel. Transfigurer un visage; l’amour, le bonheur, un sourire transfigure. Elle était au milieu du salon, debout près de son mari, dans cette tenue éblouissante qui la transfigurait (Fromentin, Dominique, 1863, p. 119).Elle me disait: « Soit, tu n’es pas jolie. Mais qu’est-ce que la beauté? Un rayon d’intelligence peut transfigurer un visage imparfait et le rendre digne d’être adoré » (Montherl., Celles qu’on prend, 1950, II, 1, p. 792).
− Au passif. Être transfiguré par un sentiment. [Christophe] était transfiguré par l’amitié; il avait une expression de joie, de confiance, de jeunesse, qu’on ne lui avait jamais vue (Rolland, J.-Chr., Maison, 1909, p. 938).
− Fréq. au part. passé. [Il] se redressait avec lenteur, l’expression transfigurée, les yeux rayonnants (Châteaubriant, Lourdines, 1911, p. 282).
− Empl. pronom. La physionomie, le visage se transfigure. La face épaisse et suante de l’abbé Godard se transfigurait d’une bonté exquise (Zola, Terre, 1887, p. 59).Je vis dans son regard briller une lueur d’orgueil. Et son corps se redressait, se transfigurait presque (Mirbeau, Journal femme ch., 1900, p. 306).
b) RELIG. CHRÉT. Transformer en donnant un aspect glorieux et éclatant.
− Au part. passé. [En parlant du Christ] Revêtu d’un éclat surnaturel et glorieux. C’est Jésus transfiguré qui vient de quitter Élie sur le Thabor (Psichari, Voy. centur., 1914, p. 217).
− Empl. subst. Celui qui a subi la transfiguration. Est-ce un transfiguré qui part et ressuscite, Qui monte, délivré de la terre, emporté Sur un char volant fait d’extase et de clarté (Hugo, Légende, t. 2, 1859, p. 812).
− Empl. pronom. Notre seigneur se transfigura sur le mont Thabor (Ac.1798-1935).P. anal. Le chevalier de Vimy cessait de paraître humain pour se transfigurer dans la soudaine magnificence de sa voix prophétique (Adam, Enf. Aust., 1902, p. 269).

2. Au fig. Changer le caractère, la nature d’une personne en lui donnant de l’éclat, une dignité nouvelle ou hors du commun. Il fera de son deuil le point de départ d’une ascension spirituelle (…) non pas, comme Nerval, pour transfigurer la femme aimée et lui donner figure d’ange intercesseur (Béguin, Âme romant., 1939, p. 352).Je me sens un tel feu et une telle âme en moi, une si haute passion enfin me transfigure que je m’estime assez haut pour mériter Julia (Camus, Dév. croix, 1953, 1rejournée, p. 533).
− Au part. passé. L’Europe, en quelques heures, désorganisée, aussitôt réorganisée; transfigurée, équipée, ordonnée à la guerre (Valéry, Variété IV, 1938, p. 69).
− Empl. pronom. Montrer au monde comment l’homme pouvait se transfigurer par la foi et l’amour (Montalembert, Ste Élisabeth, 1836, p. XXIX).Depuis la Révolution, la femme a encore grandi; elle s’est transfigurée, idéalisée (Goncourt, Ch. Demailly, 1860, p. 251).
C. − [L’obj. désigne un inanimé]
1. Changer l’aspect d’une chose en lui donnant de l’éclat, un merveilleux inhabituel ou étrange. La lumière transfigure; transfigurer le monde, l’univers. Qu’est-ce qui transfigure ainsi le boulevard? L’allure des passants n’est presque pas physique; ce ne sont plus des mouvements, ce sont des rythmes (Romains, Vie unan., 1908, p. 39).Une magie poétique transfigure tout, dans une extase qui s’accroît jusqu’à l’éclosion des suprêmes clartés (Béguin, Âme romant., 1939, p. 175).
− Au part. passé. Tout ce paysage paisible lui apparut transfiguré dans la lumière immobile (Bernanos, Joie, 1929, p. 604).
− Empl. pronom. Tout ce paysage d’or pâlit, se transfigure, s’évapore, se féerise et se pastellise comme dans un feu de Bengale vague et s’évanouissant dans un rêve (Goncourt, Journal, 1864, p. 103).

2. Au fig. Changer le caractère, la nature de quelque chose en exaltant, en sublimant. Transfigurer l’existence, le réel; transfigurer la souffrance en joie. C’est tout, en lui, que j’aime. (…) Il rehausse la vie de tous les jours, la transfigure, comme il transfigure tout (Van der Meersch, Empreinte dieu, 1936, p. 134).Il suffit d’une grâce toute simple et d’un tout simple enchantement pour transfigurer soudain la malveillance en bienveillance (Jankél., Je-ne-sais-quoi, 1957, p. 198).
− Au part. passé. Réalité transfigurée. Ces rêves qui ne sont que les souvenirs déformés ou transfigurés des obsessions d’une journée laborieuse (Baudel., Paradis artif., 1860, p. 391).
− Empl. pronom. Un chez soi, un foyer, une femme… Oh! La vie s’est transfigurée (Michelet, Peuple, 1846, p. 99).
REM. 1.
Transfigurant, -ante, part. prés. en empl. adj.Qui transfigure. Armand faillit passer sans le reconnaître dans cette féerie transfigurante le vieux vantail branlant qui était rose en plein jour (Aragon, Beaux quart., 1936, p. 169).
2.
Transfiguratif, -ive, adj.,rare. Qui transfigure. Synon. transfigurateur.Communications émotives et transfiguratives à travers l’expression des arts (Bremond, Poés. pure, 1926, p. 109).
Prononc. et Orth.: [tʀ ɑ ̃sfigyʀe], (il) transfigure [-figy:ʀ]. Att. ds Ac. dep. 1694. Étymol. et Hist. 1. a) Ca 1165 trans. « transformer, métamorphoser » (Benoît de Ste-Maure, Troie, éd. L. Constans, 29976); b) ca 1245 spéc. se transfigurer (du Christ au Mont Thabor) (Philippe Mousket, Chron., 10963 ds T.-L.); 2. a) 1610 p. ext. (P. de Deimier, L’Académie de l’Art poétique, p. 103: transfigurer ainsi les dialectes d’un langage); b) 1615 pronom. (A. de Montchrestien, Traicté d’œconomie politique, p. 47). Empr. au lat.transfigurare « transformer, métamorphoser, changer une chose en une autre » (de trans « au-delà, par delà » et figura « figure »). Fréq. abs. littér. Transfigurer: 322. Transfiguré: 270. Fréq. rel. littér.: xixes.: a) 104, b) 404; xxes.: a) 466, b) 782. Transfiguré : xixes.: a) 179, b) 388; xxes.: a) 424, b) 531. Bbg. Renson 1962, pp. 381-383., – exégétik que PRODUCTIVE, ou plutôt LE TOUT ENSEMBLE …{ bien vu} !.)
Quand Raymond Abello parle de ”LA FIN DE L’éSOTéRISME”, il faut prendre le MOT ”FIN” dans UN DOUBLE SENS & l’INTERROGATION QU’IL POSE dans ce livre est DOUBLE éGALEMENT : quel est l’OBJET, le BUT keu se propose l’éSOTéRISME ? Mais, EN ATTEIGNANT CE BUT, NE DISPARAIT-IL PAS EN TANT QUE TEL !!!

1+2+3+4+5+……. = -1/12

Sommaire
Henri Poincaré


poutine le sanguinaire qui croit que l’Allemagne de l’est et l’urss existent encore !
C’est grâve docteur ?
Henri Poincaré.
| Fauteuil 24 de l’Académie française | |
|---|---|
| 5 mars 1908 – 17 juillet 1912 | |
| Sully PrudhommeAlfred Capus | |
| Président de l’Académie des sciences | |
| 1er janvier – 31 décembre 1906 | |
| Louis Joseph TroostAuguste Chauveau | |
| Président Société mathématique de France | |
| 1900 | |
| Émile GuyouMaurice d’Ocagne | |
| Président Société mathématique de France | |
| 1886 | |
| Paul AppellGeorges-François Fouret (d) |
| Naissance | 29 avril 1854 Nancy |
|---|---|
| Décès | 17 juillet 1912 (à 58 ans) 5e arrondissement de Paris |
| Sépulture | Cimetière du Montparnasse |
| Nom de naissance | Jules Henri Poincaré |
| Nationalité | Française |
| Domicile | France |
| Formation | École polytechnique École des Mines Faculté des sciences de Paris |
| Activité | Mathématicien, physicien et philosophe |
| Père | Émile-Léon Poincaré |
| Fratrie | Aline Boutroux (d) |
| Conjoint | Louise Poulain d’Andecy (d) |
| Enfants | Jeanne Poincaré (d) Léon Poincaré (d) |
| Parentèle | Nicolas Poincaré (arrière-petit-fils) Raymond Poincaré (cousin germain paternel) Lucien Poincaré (cousin germain paternel) |
| A travaillé pour | Université de Paris École polytechnique |
|---|---|
| Domaine | Optique, calcul infinitésimal, théorie du chaos, théorie de la relativité, topologie, géométrie hyperbolique |
| Maître | Charles Hermite |
| Directeur de thèse | Charles Hermite |
| Distinctions | Liste détaillée |
| Archives conservées par | Musée Boerhaave (BOERH a 413)[1] |


LINDSEY
Superbe danseuse violoniste

Henri Poincaré, né le 29 avril 1854 à Nancy et mort le 17 juillet 1912 à Paris, est un mathématicien, physicien, ingénieur et philosophe des sciences français, souvent considéré comme l’un des derniers esprits universels, tant ses contributions couvrent de nombreux domaines scientifiques.
Issu d’une famille bourgeoise et intellectuelle, son père, Léon Poincaré, est professeur de médecine à la faculté de Nancy, et son cousin Raymond Poincaré deviendra président de la République française. Dès son plus jeune âge, Henri montre une précocité intellectuelle remarquable, notamment en mathématiques, domaine dans lequel il excelle rapidement. Il poursuit des études brillantes à l’École polytechnique puis à l’École des Mines, où il se forme comme ingénieur tout en cultivant sa passion pour les mathématiques. Très vite, il se distingue par son esprit créatif et sa capacité à aborder des problèmes complexes sous des angles inédits.
Ses travaux en mathématiques appliquées, en particulier sur les fonctions fuchsiennes, posent les bases de la théorie des fonctions automorphes, influençant profondément le développement de l’analyse mathématique. L’une de ses contributions majeures réside dans la fondation de la topologie algébrique, où il introduit le concept de la « classification des surfaces » et la notion de groupe fondamental. Ses recherches sur le problème des trois corps, un problème classique de la mécanique céleste, le conduisent à découvrir ce qui est aujourd’hui connu sous le nom de « chaos déterministe », ouvrant la voie à la théorie du chaos.

En physique, il est l’un des pionniers de la relativité restreinte, indépendamment de Lorentz et avant Einstein, introduisant des concepts cruciaux tels que la convention de la simultanéité et la relativité du temps.

Il est également très impliqué dans la vie académique et scientifique, occupant plusieurs postes prestigieux, dont celui de président de l’Académie des sciences, et il est élu membre de l’Académie française en 1908.
Biographie
GEO de novembre

Henri Poincaré est le fils d’Émile Léon Poincaré, doyen de la faculté de médecine de Nancy, et de son épouse Marie Pierrette Eugénie Launois. Il est le neveu d’Antoni Poincaré, ce qui en fait le cousin germain des fils de ce dernier : l’homme politique et président de la République française Raymond Poincaré et Lucien Poincaré, directeur de l’Enseignement secondaire au ministère de l’Instruction publique et des Beaux-Arts. La sœur d’Henri, Aline Poincaré, a épousé le philosophe Émile Boutroux.
À cinq ans, il contracte la diphtérie, le laissant paralysé durant cinq mois, ce qui l’incite à se plonger dans la lecture
Élève d’exception au lycée impérial de Nancy, il obtient le 5 août 1871, le baccalauréat en lettres, mention « Bien », et le 7 novembre 1871 son baccalauréat en sciences, où il faillit être refusé à cause d’un zéro en composition de mathématiques[8]. Il semblerait qu’il soit arrivé en retard et ait mal compris le sujet, un problème sur les séries convergentes, domaine dans lequel il apportera des contributions importantes. Mais il se rattrape brillamment à l’oral et est finalement admis avec une mention « Assez Bien ».
Henri Poincaré se relève de ce mauvais pas en classes préparatoires, où il remporte deux fois consécutivement le concours général de mathématiques. Malgré son inaptitude sportive et artistique et une épreuve de géométrie descriptive qu’il aurait ratée, il se classe premier au concours d’entrée à l’École polytechnique le 2 novembre 1873. Son rang lui vaut un grade de sergent-major. À ce titre, il est « émissaire » et président de la commission des Cotes.

Il sort deuxième de l’École Polytechnique[3] en 1875 et, le 19 octobre de la même année, il entre comme élève-ingénieur à l’École des mines de Paris, étant membre du Corps des mines ; il est licencié en sciences le 2 août 1876. Il sort de l’École des mines le 11 mars 1879, classé 3e sur les trois élèves du Corps des mines. Nommé ingénieur des mines de 3e classe le 28 mars à Vesoul, il obtient, le 1er août, le doctorat ès sciences mathématiques à la faculté des sciences de Paris, et devient chargé de cours d’analyse à la faculté des sciences de Caen le 1er décembre 1879.
Deux ans plus tard, il obtient ses premiers résultats marquants en mathématiques (sur la représentation des courbes et sur les équations différentielles linéaires à coefficients algébriques), et rapidement, il s’intéresse à l’application de ses connaissances mathématiques en physique et plus particulièrement en mécanique.
Il retourne à Paris en 1881 comme maître de conférences d’analyse à la faculté des sciences de Paris.

Henri Poincaré épouse le 20 avril 1881 Louise Poulain d’Andecy (1857-1934), petite-fille d’Isidore Geoffroy Saint-Hilaire, arrière-petite-fille d’Étienne Geoffroy Saint-Hilaire. Quatre enfants naissent de cette union entre 1887 et 1893 : Jeanne (1887-1974), future épouse de Léon Daum, Yvonne (1889-1939), Henriette (1890-1970), et Léon (1893-1972), également polytechnicien (promotion 1913), ensuite ingénieur général de l’air.
Il est nommé répétiteur d’analyse à l’École polytechnique le 6 novembre 1883, charge qu’il occupe jusqu’à sa démission en mars 1897. Nommé à la chaire de « mécanique physique et expérimentale » le 16 mars 1885, il la quitte pour la chaire de « physique mathématique et de calcul des probabilités” en août 1886, succédant ainsi à Gabriel Lippmann.
Il est président de la Société mathématique de France en 1886.
Il est élu membre de l’Académie des sciences en 1887. Il devient membre du Bureau des longitudes en 1893 et est nommé ingénieur en chef des mines. En novembre 1896, il obtient la chaire « d’astronomie mathématique et de mécanique céleste » à la faculté des sciences de Paris, succédant à Félix Tisserand qui vient de mourir.
Il est sociétaire de la Société des sciences de Nancy et membre associé de l’académie de Stanislas

Il est à nouveau président de la Société mathématique de France en 1900.
Il est président de la Société astronomique de France de 1901 à 1903[18].
Il est, en 1901, le premier lauréat de la médaille Sylvester de la Royal Society. Il est président de la Société française de physique en 1902.
Le 1er octobre 1904, Henri Poincaré est nommé professeur d’astronomie générale sans traitement à l’École polytechnique, ceci afin d’éviter la suppression de la chaire.
De 1900 à 1908, il applique ses travaux à la télégraphie sans fil, ce qui permet d’établir l’existence de régimes d’ondes entretenues

Accumulant les honneurs, il est élu à l’Académie française le 5 mars 1908, il participe à de nombreux congrès et conférences jusqu’à la fin de sa vie.
Il meurt le 17 juillet 1912 au 15 rue Monsieur (archives départementales de Paris), alors qu’il habite 63 rue Claude-Bernard, d’une embolie à la suite d’une opération pour traiter une hypertrophie de la prostate décelée dès 1908. Ses funérailles ont lieu le 19 juillet 1912 à l’église Saint-Jacques-du-Haut-Pas et sont suivies de son inhumation au cimetière Montparnasse
Poincaré et la relativité

En 1902, Poincaré publie La Science et l’Hypothèse. Même si ce livre est plus un ouvrage d’épistémologie que de physique, il appelle à ne pas considérer comme trop réels de nombreux artéfacts de la physique de son époque : le temps absolu, l’espace absolu, l’importance de l’éther. Einstein s’était particulièrement penché sur ce livre, et les idées contenues font de l’ouvrage un précurseur de la relativité restreinte.
On y trouve en particulier ce passage :

« Ainsi l’espace absolu, le temps absolu, la géométrie même ne sont pas des conditions qui s’imposent à la mécanique ; toutes ces choses ne préexistent pas plus à la mécanique que la langue française ne préexiste logiquement aux vérités que l’on exprime en français. »
En 1905, Poincaré pose les équations des transformations de Lorentz, et les présente à l’Académie des sciences de Paris le 5 juin 1905. Ces transformations vérifient l’invariance de Lorentz, achevant le travail d’Hendrik Lorentz (qui était un correspondant de Poincaré). Ces transformations sont celles qui s’appliquent en relativité restreinte, et on emploie encore aujourd’hui les équations telles que les a écrites Poincaré. Poincaré montre ainsi l’invariance des équations de Maxwell sous l’action de la transformation de Lorentz. Poincaré montre également que la transformation de Lorentz revient à une rotation entre espace et temps et qu’elle définit un groupe dont l’un des invariants est la vitesse de la lumière. Mais pour expliquer l’origine physique de ces transformations, Poincaré a recours à des contractions physiques de l’espace et du temps, conservant en références un éther et un temps absolu. Einstein, lui, part de la constance de la vitesse de la lumière (en tant que postulat) et du principe de relativité pour retrouver les mêmes transformations de Lorentz, éliminant les notions de référentiels ou horloges absolus, et faisant des différences de longueur des effets de la perspective dans un espace-temps en quatre dimensions, et non des contractions réelles

Poincaré a également proposé certaines idées sur la gravité, notamment la propagation des perturbations du champ de gravitation à la vitesse de la lumière, ce qu’il nomma « ondes gravifiques ». Sa faiblesse était de trop rechercher l’analogie avec l’électromagnétisme en cherchant une nouvelle loi de gravitation qui soit invariante par les transformations de Lorentz. Paul Langevin note que Poincaré a trouvé « plusieurs solutions possibles qui présentent toutes ce caractère commun que la gravitation se propage avec la vitesse de la lumière, du corps attirant au corps attiré, et que la loi nouvelle permet de représenter les mouvements des astres mieux encore que la loi ordinaire puisqu’elle atténue les divergences existant encore entre celle-ci et les faits, dans le mouvement du périhélie de Mercure, par exemple. »
Si les physiciens de l’époque étaient parfaitement au courant des travaux de Poincaré, le grand public l’a ensuite presque oublié, alors que le nom d’Einstein est aujourd’hui connu de tous. Récemment, quelques voix ont cherché à rappeler le rôle de Poincaré, mais d’autres sont allés plus loin, cherchant à faire de Poincaré l’auteur de la théorie de la relativité. Cette controverse sur la paternité de la relativité est d’autant plus délicate que les conflits politiques se mêlent aux questions de lecture des articles de physique.
Mathématiques

Poincaré est le fondateur de la topologie algébrique. Ses principaux travaux mathématiques ont eu pour objet la géométrie algébrique, des types de fonctions particuliers – les fonctions dites « automorphes » (il découvre les fonctions fuchsiennes et kleinéennes), les équations différentielles… La notion de continuité est centrale dans son travail, autant par ses répercussions théoriques que pour les problèmes topologiques qu’elle entraîne.
« […] l’un des derniers représentants de cette science à en avoir eu une totale maîtrise dans l’ensemble des domaines, y compris dans ses applications en astronomie et en physique[25]. »
Fondements des mathématiques

Pendant les six dernières années de sa vie (à partir de 1905), Poincaré participe activement aux débats sur les fondements qui traversaient à l’époque la communauté mathématique. Il n’a jamais essayé d’y contribuer sur le plan technique, mais certaines de ses idées ont eu une influence indéniable. L’un de ses contradicteurs, Bertrand Russell, écrira en 1914 : « Il n’est pas possible d’être toujours juste en philosophie ; mais les opinions de Poincaré, justes ou fausses, sont toujours l’expression d’une pensée puissante et originale, servie par des connaissances scientifiques tout à fait exceptionnelles » Entre autres, à cause de son refus d’accepter l’infini actuel, c’est-à-dire la possibilité de considérer l’infini comme une entité achevée et non simplement comme un processus qui peut se prolonger arbitrairement longtemps, Poincaré est considéré par beaucoup d’intuitionnistes comme un précurseur. Poincaré n’a cependant jamais remis en cause le tiers exclu, et rien n’indique qu’il aurait pu adhérer à une refondation aussi radicale des mathématiques que celle que proposera Luitzen Egbertus Jan Brouwer.

La position de Poincaré a évolué. Dans une période précédente, il s’est intéressé aux travaux de Georg Cantor, dont les travaux sur la construction des réels et la théorie des ensembles s’appuient de façon essentielle sur un infini actuel, au point de superviser la traduction en français d’une partie des articles de ce dernier (en 1871, 1883…), et d’utiliser ses résultats dans son mémoire sur les groupes kleinéens (1884). Il s’intéresse également aux travaux de David Hilbert sur l’axiomatisation : il fait, en 1902, une recension soignée et très louangeuse des Fondements de la géométrie (1899).
En 1905 et 1906, Poincaré réagit, de façon assez polémique, à une série d’articles de Louis Couturat sur les « principes des mathématiques » dans la Revue de métaphysique et de morale, articles qui rendaient compte des Principles of Mathematics de Bertrand Russell (1903). Russell finira par intervenir lui-même dans le débat.
Poincaré, contrairement à ce qu’on dit souvent, n’a jamais partagé ce que l’on appelle de manière vague l’intuitionnisme kantien. Quand il évoque l’intuition (La valeur de la science, ch. 1), ce terme signifie « image » ou « modèle ». Sa conception de l’expérience n’a pas grand-chose à voir avec celle de Kant : ni l’espace ni le temps ne sont des « formes a priori », car l’expérience n’est que l’occasion à partir de laquelle l’espace représenté est mis en relation avec l’espace comme continuum amorphe : « L’expérience n’a donc joué qu’un seul rôle, elle a servi d’occasion. Mais ce rôle n’en était pas moins très important ; et j’ai cru nécessaire de le faire ressortir. Ce rôle aurait été inutile s’il existait une « forme a priori » s’imposant à notre sensibilité et qui serait l’espace à trois dimensions. » (La valeur de la science, ch. 4, § 6). Quand Poincaré évoque l’idée de commodité, il est plus proche des empiristes que des idéalistes : l’idée de vérité n’a plus grand-chose à voir avec l’idée de jugement synthétique a priori, parce qu’on « choisit » ses principes ou axiomes, tout comme on choisit les faits dans les sciences de la nature. Le principe de récurrence semble n’avoir d’autre but que de montrer la non-pertinence du logicisme, qui fait de la déduction le ressort central de la démonstration mathématique.

Pour lui, c’est précisément le cas du principe de récurrence, qu’il nomme également « principe d’induction », en ce qu’il s’oppose à la déduction, et qu’il refuse de considérer comme le fruit d’un jugement purement analytique, comme le sont pour lui les raisonnements logiques. Ceci l’oppose à Russell (et, à travers lui, à Gottlob Frege, que Poincaré méconnaît), qui veut réduire les mathématiques à la logique, cela l’oppose aussi à ceux qu’il appelle les cantoriens, comme Ernst Zermelo, et dont il distingue en partie Hilbert. À ces derniers, il reproche l’usage de l’infini actuel, à travers leur façon de « passer du général au particulier », par exemple le fait de supposer l’existence d’ensembles infinis pour définir l’ensemble des entiers naturels, alors que, pour lui, les entiers naturels sont premiers. Il refuse ce qu’il appelle les définitions non prédicatives (voir paradoxe de Richard), qui, pour définir un ensemble E, font appel à « la notion de l’ensemble E lui-même » (typiquement, la définition actuelle en théorie des ensembles de N, l’ensemble des entiers naturels, comme intersection des ensembles contenant 0 et clos par successeur, est non prédicative au sens de Poincaré, puisque N fait partie de ces derniers). Les objections de Poincaré, par les réactions qu’elles ont nécessitées, ont joué un rôle non négligeable dans la naissance de la logique mathématique et de la théorie des ensembles, même si ses idées ont eu finalement relativement peu de succès. Elles influencent tout de même notablement l’intuitionnisme de Brouwer et ses successeurs (qui reste très marginal chez les mathématiciens), et ont connu des développements en théorie de la démonstration à partir des années 1960.
Problème des trois corps
Article détaillé : Problème des trois corps.

Alors qu’il étudie le problème des trois corps dans le cadre d’un concours (1888) organisé par Gosta Mittag-Leffler[f], Poincaré démontre qu’il n’y a pas de solutions générales, un résultat qu’avait déjà obtenu Heinrich Bruns. Il découvre également l’existence de solutions apériodiques. Un historique très détaillé de la contribution de Poincaré au problème des trois corps a été publié par June Barrow-Green
Il reprend cette étude dans Les méthodes nouvelles de la mécanique céleste (trois volumes publiés entre 1892 et 1899). Dans le volume III, Poincaré y découvre les orbites homoclines et hétéroclines, au voisinage desquelles il remarque qu’il y a une grande sensibilité aux conditions initiales. Cette propriété est à la base des comportements chaotiques qui seront découverts par Edward Lorenz et par Otto Rössler
Dans le cadre de ces études des équations différentielles et du problème des trois corps, Poincaré introduit un grand nombre de concepts de la théorie du chaos : mentionnons les différents types de points singuliers (nœud, col, foyer et centre), la notion de bifurcation, de cycle limite, de section de Poincaré, d’application de premier retour (encore appelée application de Poincaré), etc. Il comprend notamment que l’étude de ces solutions apériodiques passe par l’étude des orbites périodiques qui se développent dans leur voisinage
Conjecture de Poincaré
Article détaillé : Conjecture de Poincaré.
Posée en 1904 par Poincaré, la conjecture portant son nom était un problème de topologie énoncé sous cette forme par son auteur :

« Considérons une variété compacte V à 3 dimensions sans bord. Est-il possible que le groupe fondamental de V soit trivial bien que V ne soit pas homéomorphe à une sphère de dimension 3 ? »
En l’an 2000, l’institut Clay plaça la conjecture parmi les sept problèmes du prix du millénaire. Il promit un million de dollars américains à celui qui démontrerait ou réfuterait la conjecture. Grigori Perelman a démontré cette conjecture en 2003, et sa démonstration fut validée en 2006. Mais le chercheur a refusé aussi bien la médaille Fields que le million de dollars.
Attributs d’un génie
Deux biographes esquissent son portrait et fournissent des anecdotes : les mathématiciens Paul Appell et Gaston Darboux. Les deux biographes s’accordent à dire que Poincaré était un lecteur insatiable et qu’il mémorisait facilement ce qu’il lisait. Étant myope, il voyait mal le tableau noir et développa ainsi une sorte de mémoire auditive qui lui permettait de se souvenir des cours sans prendre de notes. Il ne dessinait pas très bien, mais faisait preuve de beaucoup d’imagination spatiale grâce à une solide vision intérieure, qui lui permettait de se plonger dans les méandres de la géométrie et de la topologie. Si un problème l’intéressait, il faisait abstraction de tout le reste : rien d’autre ne semblait lui importer et il en oubliait parfois de manger. Il pouvait effectuer ses calculs mentalement, au cours d’une promenade, et ne les couchait sur papier que lorsqu’il savait précisément ce qu’il devait faire. C’était un homme impatient qui écrivait vite. Lorsqu’il avait compris ou résolu un problème, il en écrivait la solution à toute vitesse, relisant et révisant à peine ce qu’il avait écrit. Il commit ainsi d’importantes erreurs dans certains de ses articles.

Poincaré ne brillait pas par ses aptitudes physiques bien qu’il fût un bon danseur. Il aimait la musique, mais ne semblait pas avoir de don particulier pour l’interpréter et ne jouait d’aucun instrument. Dès son plus jeune âge, il s’avéra être un écrivain doué et créa des œuvres de théâtre qui représentaient ses proches et ses amis. Il n’était toutefois pas doué de ses mains. Il tenait en estime la physique expérimentale et s’y intéressait, mais il ne fit aucune expérience originale. Poincaré se distinguait surtout grâce à son intelligence exceptionnelle. Dès sa jeunesse, il pouvait résoudre des problèmes très complexes. Au premier abord, son côté introspectif pouvait donner l’impression qu’il était un jeune homme hautain. Cependant, il fut rapidement apprécié de ses camarades, car il était toujours prêt à aider les autres qui butaient sur un problème, et était généralement un bon camarade.

Il était pieux dans sa jeunesse et à l’adolescence, mais avait cessé d’être croyant à l’âge de dix-huit ans. Il était progressiste concernant les problématiques liées à l’éducation ou à la participation de la femme à la vie politique. Il se méfiait de l’Église catholique, de ses prises de position anti-intellectuelles[source insuffisante] et de sa quête permanente d’influence sur la vie sociale et politique du pays. Il fut l’exemple type de ce que l’on pourrait appeler la « morale laïque » de la République française. La droiture, la sincérité, la loyauté, le dévouement au service de la société et la quête du bien commun étaient pour lui des valeurs suprêmes et universelles[34],[35].
Philosophe et homme de lettres
Poincaré est aussi le dernier à avoir la double spécificité de comprendre l’ensemble des mathématiques de son époque et d’être en même temps un penseur philosophique. On le considère comme un des derniers grands savants universels[36], du fait de ses recherches dans des domaines transversaux (physique, optique, astronomie…), et de son attitude scientifique fondée sur une esthétique de la science et du nombre, à rapprocher de celle des anciens Grecs.
Il a œuvré toute sa carrière durant à la vulgarisation de ses résultats et des grands travaux de la science, attitude qui sera reprise par des physiciens ultérieurs.
Avec La Science et l’Hypothèse, devenu un classique de la philosophie des sciences du XXe siècle, il intéresse le monde artistique, notamment les cubistes, et donne des clés de compréhension aux géométries non euclidiennes.
De manière plus anecdotique, on peut noter que Poincaré aurait écrit un roman de jeunesse

Participation à la vie publique
Article détaillé : Affaire Dreyfus.
En 1899, Henri Poincaré adresse une lettre au Conseil de guerre de Rennes, chargé de juger le capitaine Dreyfus, critiquant les méthodes d’analyse du bordereau qui semble accuser Dreyfus
En 1904, à la demande de la Cour de cassation, Poincaré signe avec Darboux et Appell un rapport, qui sera versé au procès en révision de Dreyfus par cette même cour en 1906. Ce rapport, principalement rédigé par Poincaré, dénonce et corrige les erreurs mathématiques d’analyse du bordereau, et notamment l’utilisation du théorème de Bayes
Honneurs et hommages
Honneurs

- Lauréat du concours général, en mathématiques
- Prix du roi Oscar II de Suède en 1889
- Médaille d’or de la Royal Astronomical Society (1900)
- Prix Bolyai (1905)
- Membre de l’Académie française (1908)
- Médaille Bruce (1911)
- Commandeur de la Légion d’honneur
Pour l’ensemble de ses travaux, Poincaré fut pressenti à plusieurs reprises au prix Nobel de physique
Hommages

- L’astéroïde « (2021) Poincaré » porte son nom.
- En 1970, l’Union astronomique internationale a attribué le nom de Poincaré à un cratère lunaire.
- Buste en bronze par le statuaire Joseph Carlier (1849-1927), érigé dans le square du lycée de Nancy par souscription des anciens élèves des lycées de Nancy, Colmar, Metz et Strasbourg en 1913.
- Le lycée Henri-Poincaré de Nancy, qu’il a fréquenté, porte son nom.
- L’institut Henri-Poincaré, maintenant au sein du Campus Curie de Sorbonne Université, est créé en 1928. L’université Henri-Poincaré à Nancy est nommée en son honneur. Les archives Henri-Poincaré (laboratoire d’histoire des sciences et de philosophie à l’Université de Lorraine) effectuent des recherches sur ses travaux. Le plus grand amphithéâtre de l’École polytechnique sur son campus de Palaiseau, d’une capacité de 780 places, porte le nom de Poincaré et est surnommé « le .K » (lire « le point K ») par les élèves de l’École.
- La poste a créé un timbre Henri Poincaré en octobre 1952.
- La centrale hydroélectrique de Châteauneuf-du-Rhône dans la Drôme au sud de Montélimar mise en service en 1958 porte son nom.
- Deux bâtiments de la Marine nationale ont porté son nom, un sous-marin de la classe 1500 tonnes (1927-1942) et un bâtiment d’essais et de mesure (BEM) (1968-1991)
- La maison Poincaré est un musée des mathématiques situé à Paris, ouvert au public en octobre 2023.
Principales publications (cours et essais)
- Sur les propriétés des fonctions définies par les équations aux différences partielles : 1re thèse, Gauthier-Villars (Paris), 1879, texte en ligne disponible sur IRIS [archive]
- Notice sur les travaux scientifiques d’Henri Poincaré, Gauthier-Villars (Paris), 1886, texte en ligne disponible sur IRIS [archive]
- Les méthodes nouvelles de la mécanique céleste, Tome 1, Gauthier-Villars (Paris), 1892, Texte en ligne disponible sur IRIS, Tome 2, Gauthier-Villars (Paris), 1893, Texte en ligne sur IRIS, Tome 3, Gauthier-Villars (Paris), 1899, Texte en ligne sur IRIS
- Analysis Situs : série d’articles, de 1895 à 1904
- Sur les propriétés des fonctions définies par les équations aux différences partielles. Propositions données par la faculté, Paris, Gauthier-Villars, 1879 (lire en ligne [archive])
- La Science et l’Hypothèse (Flammarion – Bibliothèque de philosophie scientifique – 1902)
- La Valeur de la Science (Flammarion – Bibliothèque de philosophie scientifique – 1905)
- Cours d’astronomie générale : École polytechnique : 1re division : 1906-1907, École polytechnique (Paris), 1907, texte en ligne disponible sur IRIS [archive]
- La Théorie de Maxwell et les oscillations hertziennes. La Télégraphie sans fil, Scientia, 1904.
- Science et Méthode (Flammarion – Bibliothèque de philosophie scientifique – 1908)
- Savants et écrivains (Flammarion – 1910)
- Dernières Pensées (Flammarion – Bibliothèque de philosophie scientifique – 1913), réédité par Flammarion, complété d’autres articles en appendice à partir de la seconde édition de 1926.
- Ce que disent les choses, (1911), Hachette : cinq chapitres publiés dans la revue pour enfants Au seuil de la vie (Hachette, 1910) et repris par Hachette en 1911 dans l’ouvrage éponyme Ce que disent les choses. Réédité en 2010 chez Hermann, Paris (voir bibliographie).
- Leçons sur les hypothèses cosmogoniques (Poincaré, 1911), une partie étant consacrée aux travaux d’Émile Belot.
- Cours de la faculté des sciences de Paris publiés par l’Association amicale des élèves et anciens élèves de la faculté des sciences – Cours de mécanique physique et expérimentale :
- Cours de la faculté des sciences de Paris publiés par l’Association amicale des élèves et anciens élèves de la faculté des sciences – Cours de physique mathématique :
- Leçons sur la théorie mathématique de la lumière professées pendant le premier semestre 1887-1888 [archive],
- Électricité et optique, la lumière et les théories électrodynamiques, leçons professées en 1888, 1890 et 1899 (Carré et Naud- 1901)
- Thermodynamique : leçons professées pendant le premier semestre 1888-89 [archive] – Rédaction de J. Blondin, agrégé de l’université – Paris Gauthier-Villars 1908 – Réimpression 1995 des Éditions Jacques Gabay.
- Capillarité : Leçons professées pendant le deuxième semestre 1888-1889 [archive],
- Leçons sur la théorie de l’élasticité (Carré – 1892)
- Théorie mathématique de la lumière II : nouvelles études sur la diffraction.-Théorie de la dispersion de Helmholtz : Leçons professées pendant le premier semestre 1891-1892 [archive],
- Théorie des tourbillons, leçons professées pendant le deuxième semestre 1891-1892 (Carré et Naud- 1893)
- Les oscillations électriques, leçons professées pendant le premier trimestre 1892-1893 (Carré et Naud- 1900)
- Théorie analytique de la propagation de la chaleur, leçons professées pendant le premier semestre 1893-1894 (Carré – 1895)
- Calcul des probabilités, leçons professées pendant le deuxième semestre 1893-1894 (Carré et Naud- 1896)
- Théorie du potentiel newtonien, leçons professées pendant le premier semestre 1894-1895 (Carré et Naud – 1899)
- Cours de la faculté des sciences de Paris – Cours de mécanique céleste :
- Rapports présentés au congrès International de Physique réuni à Paris en 1900 sous les auspices de la Société française de physique rassemblés et publiés par Ch.-Ed.Guillaume et H.Poincaré, secrétaires généraux du congrès – trois volumes in-8° avec figures ; Paris, Gauthier-Villars – 1900
- Œuvres publiées sous les auspices de l’Académie des Sciences en onze volumes, compilations d’articles publiés dans divers revues scientifiques, Éditions Jacques Gabay.[1] [archive]
Notes et références
Notes

- Nicolas Poincaré est donc polytechnicien de la promotion 1845, né en 1825 et mort en 1911.
- Paul Appell entre en classe de mathématiques spéciales à la même époque.
- En tant qu’ingénieur des mines, il mènera l’enquête sur l’explosion ayant eu lieu le 1er septembre 1879 dans le Puits du Magny, causant la mort de seize mineurs.
- Étienne Klein précise qu’Einstein a même fait de ce livre un thème de discussion avec ses amis de l’« académie Olympia ».
- Concours lancé mi-1885 ; limite de soumission le 1er juin 1888 ; résultat prononcé le 20 janvier 1889
- Avec comme jury Mittag-Leffler lui-même, Charles Hermite et Karl Weierstrass
Références
- « https://rijksmuseumboerhaave.nl/over-ons/bibliotheek/ [archive] »
- « 127e congrès, Nancy, 2002 [archive] », sur le Comité des travaux historiques et scientifiques (consulté le ).
- Ouvrir la « Page d’accueil [archive] », sur le site de la bibliothèque de l’École polytechnique, Palaiseau (consulté le ), sélectionner l’onglet « Catalogues de la BCX → Famille polytechnicienne », effectuer la recherche sur « Poincaré Henri », résultat obtenu : « Poincaré, Jules Henri (X 1873 ; 1854-1912) ».
- « Henri Poincaré (1854-1912) [archive] », sur les Annales des Mines (consulté le ).
- Ouvrir la « Page d’accueil [archive] », sur le site de la bibliothèque de l’École polytechnique, Palaiseau (consulté le ), sélectionner l’onglet « Catalogues de la BCX → Famille polytechnicienne », effectuer la recherche sur « Poincaré Nicolas », résultat obtenu : « Poincaré, Nicolas Antonin Hélène (X 1845 ; 1825-1911) ».
- Aline Boutroux, Vingt ans de ma vie, simple vérité : la jeunesse de Henri Poincaré racontée par sa sœur, 1854-1878, Paris, Hermann, 2012, 360 p. (ISBN 978-2-7056-8278-1).
- Jean-Marc Ginoux et Christian Gerini, Henri Poincaré : une biographie au(x) quotidien(s), Paris, Ellipses Marketing, 2012, 298 p. (ISBN 978-2-7298-7407-0 et 2-7298-7407-0), p. 304.
- Paul Appell, Henri Poincaré, Plon, 1925, 119 p. (lire en ligne [archive] ), p. 19« Nous signalons encore une fois ce zéro à l’écrit en mathématiques au baccalauréat ; il s’agissait d’une composition sur une question du programme. Si les examinateurs n’avaient pas su ce qu’était Henri Poincaré, ils ne l’auraient… »
- Darboux 1913.
- PoinK, GénéK [archive].
- Henri Poincaré sur les Annales des mines [archive].
- Relevé de notes de Henri Poincaré à l’École des mines [archive].
- Laurent Rollet, « Jeanne Louise Poulain d’Andecy, épouse Poincaré (1857-1934) », Bulletin de la Sabix. Société des amis de la Bibliothèque et de l’Histoire de l’École polytechnique, no 51, 15 novembre 2012, p. 18–27 (ISSN 0989-3059, DOI 10.4000/sabix.1131, lire en ligne [archive], consulté le )
- Laurent Mazliak. « Poincaré’s Odds ». In : Poincaré 1912-2012 : Poincaré Seminar 2012. B. Duplantier et V. Rivasseau, Editors. T. 67. Progress in Mathematical Physics. Basel : Birkhäuser
- « Présentation de l’Académie lorraine des sciences [archive] », sur le site de l’ALS (consulté le ).
- (fr) Maubeuge, P.-L. (1961) – « Historique de la Société des Sciences de Nancy et de la Société Lorraine des Sciences », Bulletin de la Société lorraine des sciences, tome I no 1 [archive] [PDF], Nancy, p. 43
- « POINCARÉ Jules Henri [archive] », sur le site du Comité des travaux historiques et scientifiques (CTHS) (consulté le ).
- « L’Astronomie : revue mensuelle d’astronomie, de météorologie et de physique du globe et bulletin de la Société astronomique de France [archive] », sur Gallica, 1937 (consulté le )
- André Rougé, Relativité restreinte : La contribution d’Henri Poincaré, Éditions École polytechnique, 2008, p. 135.
- « Les conférences oubliées de Poincaré sur la T.S.F. [archive] », sur Bibnum (consulté le ).
- Laurent Rollet, « Un mathématicien au Panthéon, à propos de la mort d’Henri Poincaré », Colloque “ Henri Poincaré – Mathématiques et interactions des mathématiques avec les autres champs disciplinaires ”, dans le cadre du 127e Congrès National des Sociétés Historiques et Scientifiques, 2002 (lire en ligne [archive], consulté le )
- (en) V. Messager, R. Gilmore & C. Letellier, Henri Poincaré and the principle of relativity, Contemporary Physics, 53 (5), 397-415, 2012.
- Jean-Claude Boudenot (préf. Claude Cohen-Tannoudji), Comment Einstein a changé le monde, Les Ulis, EDP sciences, 2005, 187 p. (ISBN 978-2-7598-0224-1, OCLC 230760088, lire en ligne [archive]).
- La gravitation newtonienne face au principe de relativité – Relativité générale : comment l’espace-temps devint dynamique [archive].
- Gérard Besson, Christian Houzel et Michel Paty, « POINCARÉ HENRI (1854-1912) [archive] », sur Encyclopædia universalis (consulté le ).
- « To be always right is not possible in philosophy; but Poincaré’s opinions, right or wrong, are always the expression of a powerful and original mind, with a quite unrivalled scientific equipement », Bertrand Russell, préface de la traduction anglaise de Science et méthode, Londres 1914, [lire en ligne [archive]].
- D’après Pierre Dugac, préface à une édition d’un recueil des articles en français de Georg Cantor, voir le site de la BNF [archive].
- Journal des savants mai 1902, repris en appendice, dans plusieurs éditions de l’ouvrage posthume Dernières pensées à partir de 1926, voir la bibliographie.
- Tous ces articles sont parus dans la revue de métaphysique et de morale et sont accessibles en ligne sur le site de la BNF [archive].
- Jean-Christophe Yoccoz, « Une erreur féconde du mathématicien Henri Poincaré », La lettre du Collège de France [En ligne], no 28, avril 2010 (lire en ligne [archive], consulté le )Version papier : La Lettre du Collège de France no 28, Paris, Collège de France, avril 2010, p. 38-42, ISSN 1628-2329.Conférence à la Bibliothèque nationale de France le 13 avril 2005. Ce texte a été publié dans la Gazette des mathématiciens, no 107, 2006, p.19-26.
- (en) J. Barrow-Green, Henri Poincaré and the three-body problem, American Mathematical Society, 1996.
- C. Letellier, Le chaos dans la nature, Vuibert, 2006.
- Il mesurait 1,65 m et pesait environ 70 kg en 1909
- Selon l’étude psychologique de Poincaré effectuée par le docteur Édouard Toulouse, directeur du laboratoire de psychologie expérimentale de l’École des hautes études de Paris.
- Pérez Izquierdo et Prime 2018, p. 41-42/125-126
- Jean-Marc Ginoux et Christian Gérini, « Le dernier savant universel, Henri Poincaré, mort en 1912 [archive] », sur lefigaro.fr, 16 juillet 2012 (consulté le )
- Christian Houzel et Michel Paty, « POINCARÉ HENRI (1854-1912) : 3. Poincaré philosophe [archive] », sur Encyclopædia universalis (consulté le )(frais de consultation requis).
- Une ancienne version (octobre 2007) du site du lycée Henri-Poincaré.
- Xavier Verley, Poincaré ou le renouveau de la philosophie naturelle, p. 15.
- Journal électronique d’histoire des probabilités et de la statistique [archive].
- Pérez Izquierdo et Prime 2018, p. 9/13
- Décret du 14 janvier 1903
- (en-US) « Nomination Archive [archive] », sur NobelPrize.org (consulté le )
- « Net-Marine [archive] », sur netmarine.net (consulté le )
- Voir aussi : Henri Poincaré, Science et Méthode, Paris, Flammarion, 1947 (lire en ligne [archive] [PDF]), sur le portail documentaire de l’université Pierre-et-Marie-Curie.
- [PDF]« Dernières Pensées [archive] », sur l’Académie de Nancy-Metz.
Voir aussi
Sur les autres projets Wikimedia :
- Henri Poincaré, sur Wikimedia Commons
- Henri Poincaré, sur Wikisource
- Henri Poincaré, sur Wikiquote
Correspondance
- Henri Poincaré Papers, site édité par Scott A. Walter, Université de Nantes [archive]
- « Henri Poincaré Papers [archive] », sur Université de Lorraine (consulté le )
Bibliographie
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- Paul Appell, Henri Poincaré, 1925, Librairie Plon
- André Bellivier, Henri Poincaré ou la vocation souveraine, coll. « Vocations » n° IV, Gallimard, Paris, 1956.
- Aline Boutroux et Laurent Rollet (édition), Vingt ans de ma vie, simple vérité : la jeunesse d’Henri Poincaré racontée par sa sœur, 1854-1878, Paris, Hermann, 2012, 350 p. (ISBN 978-2-7056-8278-1)
- Christian Bracco et Jean-Pierre Provost, Henri Poincaré et la relativité : 1900, 1905, 1912. Trois moments de sa réflexion, ISTE Éditions, 2023, 249 p. (ISBN 978-1-78405-950-7 et 978-1-78406-950-6, présentation en ligne [archive])
- Éric Charpentier (dir.), Étienne Ghys (dir.) et Annick Lesne (dir.), L’héritage scientifique de Poincaré, Paris, Belin, coll. « Échelles », 2006, 423 p. (ISBN 978-2-7011-4332-3, OCLC 85335027)
- Charles Croix, La famille de Poincaré est-elle bourguignonne ?, dans le Pays Lorrain, 1935, p. 331-333)
- Camillo Cuvaj, A history of relativity, the role of Henri Poincaré and Paul Langevin, thèse de doctorat, 1970
- Gaston Darboux, « Éloge historique d’Henri Poincaré lu dans la séance publique annuelle du par M. Gaston Darboux, secrétaire perpétuel de l’Académie des sciences [archive] », 15 décembre 1913 (consulté le )
- Général Dassault, Henri Poincaré, Annales des Mines, octobre 1954
- Vladimir Fock, The Theory of Space Time and Gravitation, Pergamon, 1958, p. xviii, 350, 370-374
- Christian Gerini, Henri Poincaré, « Ce que disent les choses » quand Henri Poincaré écrit pour les enfants, Paris, Hermann, coll. « Histoire des sciences », 2010, 171 p. (ISBN 978-2-705-66973-7, OCLC 708353618)
- Jean-Marc Ginoux et Christian Gerini (préf. Cédric Villani), Henri Poincaré : une biographie au(x) quotidien(s), Paris, Ellipses, 2012, 298 p. (ISBN 978-2-7298-7407-0, OCLC 819206966, BNF 42747074)
- (en) Jeremy Gray, Henri Poincaré : A Scientific Biography, Princeton, Princeton University Press, 2013, 592 p. (ISBN 978-0-691-15271-4, présentation en ligne [archive]) — Voir le compte rendu de John Stillwell, « Henri Poincaré. A Scientific Biography », Notices of the AMS, vol. 61, no 4, 2014, p. 378-383 (ISSN 0002-9920, DOI 10.1090/noti1101)
- G. H. Keswani, Origin and Concept of Relativity, Parts I, II, III, Brit. J. Phil. Sci. (en) vol. 15-17, 1965-66
- Ernest Lebon, Henri Poincaré, biographie, bibliographie analytique des écrits, Paris, Gauthier-Villars, 1909 [lire en ligne [archive]]
- Jean Mawhin, Les Histoires belges d’Henri Poincaré, 1845-1912, Bruxelles, Académie royale de Belgique, coll. « L’académie en poche » (no 5), 2012, 103 p. (ISBN 978-2-8031-0308-9, OCLC 901402230)
- Michel Paty, Poincaré, Langevin et Einstein [archive], Epistémologiques, 2002
- Alberto Tomás Pérez Izquierdo et Simon Prime (trad.), L’invention de la topologie : Poincaré, Barcelone, RBA Coleccionables, 2018, 174 p. (ISBN 978-84-473-9315-2).

- André Rougé, Relativité restreinte : la contribution d’Henri Poincaré, Palaiseau, École polytechnique, coll. « Histoire de la physique », 2008, 276 p. (ISBN 978-2-7302-1525-1, OCLC 436981772, BNF 41470293, lire en ligne [archive]).
- Jean-Jacques Samueli et Jean-Claude Boudenot, H. Poincaré (1854-1912) : physicien, Paris, Ellipses, 2005, 152 p. (ISBN 978-2-7298-2245-3, BNF 39937525).
- Anne-Françoise Schmid, Henri Poincaré : Les sciences et la philosophie, Paris/Montréal (Québec)/Budapest etc., L’Harmattan, 2001, 256 p. (ISBN 2-7475-0440-9, lire en ligne [archive])
- Édouard Toulouse, Enquête médico-psychologique sur la supériorité intellectuelle : Henri Poincaré. Paris, Flammarion, 1910, 204 pages
- (en) Ferdinand Verhulst, Henri Poincaré : impatient genius, New York, Springer, 2012 (ISBN 978-1-4614-2407-9 et 978-1-461-42406-2, OCLC 806458685, lire en ligne [archive]). (Selon Jean Mawhin : « Ferdinand Verhulst has written a true scientific biography, introducing Poincaré the man, his cultural milieu, and his mathematics. This book shows why, a century after his death, Poincaré’s ideas still shape a substantial part of the mathematical sciences. »)
- Xavier Verley, Poincaré ou le renouveau de la philosophie naturelle, Paris, Les Belles Lettres, coll. « Figures du savoir » (no 46), 2009, 223 p. (ISBN 978-2-251-76065-0, BNF 42083841)
- Henri Poincaré, l’œuvre scientifique, l’œuvre philosophique, par Vito Volterra, Jacques Hadamard, Paul Langevin et Pierre Boutroux, Librairie Félix Alcan, 1914
- Henri Poincaré, l’œuvre mathématique, par Vito Volterra
- Henri Poincaré, le problème des trois corps, par Jacques Hadamard
- Henri Poincaré, le physicien, par Paul Langevin
- Henri Poincaré, l’œuvre philosophique, par Pierre Boutroux
Articles connexes
- Application de Poincaré
- Archives Henri-Poincaré – Philosophie et Recherches sur les Sciences et les Technologies
- Conjecture de Poincaré
- Demi-plan de Poincaré
- Disque de Poincaré
- Dualité de Poincaré
- Espace dodécaédrique de Poincaré
- Formule du crible de Poincaré
- Géométrie non euclidienne
- Groupes de Poincaré
- Inégalité de Poincaré
- Lemme de Poincaré
- Lemme de Poincaré-Volterra
- Sphère d’homologie de Poincaré
- Sphère de Poincaré
- Théorèmes de Poincaré
- Léon Daum
- Poincaré et la popularisation de la 4e dimension
- Prix Henri-Poincaré
- Liste de sujets portant le nom de Henri Poincaré
Liens externes
- « Henri Poincaré, à la ligne ! » [archive], La Méthode scientifique, France Culture, 20 janvier 2022.
- Henri Poincaré, mathématicien, physicien et philosophe – Animation CNRS/sagascience (2012) [archive]
- Bibliographie de Poincaré [archive] sur le site Henri Poincaré Papers [archive], Université de Nantes
- Henri Poincaré sur le site de l’ENS [archive]
- Consulter les travaux de Henri Poincaré dans la bibliothèque numérique de l’École des mines [archive]
- Poincaré et la T.S.F., conférence de 1908 en ligne et commentée sur le site BibNum [archive].
- « Centrale hydroélectrique Henri Poincaré [archive] » sur le site La Région Auvergne-Rhône-Alpes
Notices et ressources
- Ressources relatives à la recherche :
- Ressource relative à la littérature :
- Ressource relative à l’astronomie :
- Ressource relative à la santé :
- Ressource relative à plusieurs domaines :
- Ressource relative à la vie publique :
- Ressource relative à la musique :
- Notices dans des dictionnaires ou encyclopédies généralistes :
- Britannica [archive]
- Brockhaus [archive]
- Den Store Danske Encyklopædi [archive]
- Deutsche Biographie [archive]
- Enciclopedia italiana [archive]
- Enciclopedia De Agostini [archive]
- Gran Enciclopèdia Catalana [archive]
- Hrvatska Enciklopedija [archive]
- Internetowa encyklopedia PWN [archive]
- Larousse [archive]
- Nationalencyklopedin [archive]
- Store norske leksikon [archive]
- Treccani [archive]
- Universalis [archive]
- Visuotinė lietuvių enciklopedija [archive]
- Portail des mathématiques
- Portail de la physique
- Portail de l’astronomie
- Portail de la philosophie
- Portail de l’Académie française
- Portail de l’histoire des sciences
- Portail de Nancy
- Portail de la Lorraine
- Portail de la France
- Henri Poincaré
- Mathématicien français du XIXe siècle
- Mathématicien français du XXe siècle
- Physicien français du XIXe siècle
- Physicien français du XXe siècle
- Philosophe des sciences
- Philosophe des mathématiques
- Écrivain scientifique français
- Président de la Société astronomique de France
- Lauréat de la médaille Bruce
- Lauréat de la médaille d’or de la Royal Astronomical Society
- Lauréat du prix Poncelet
- Lauréat du prix Jean-Reynaud
- Lauréat de la médaille Sylvester
- Commandeur de la Légion d’honneur promu en 1903
- Membre de l’Académie des sciences (France)
- Membre de l’Académie française
- Membre de l’Académie de Caen
- Membre de l’Académie de Stanislas
- Membre de l’Académie lorraine des sciences
- Membre de l’Académie bavaroise des sciences
- Membre de l’Académie royale néerlandaise des arts et des sciences
- Membre de l’Académie hongroise des sciences
- Professeur à l’École polytechnique
- Professeur à la faculté des sciences de Paris
- Ingénieur du corps des mines
- Élève du lycée Henri-Poincaré
- Élève de l’École des mines de Paris
- Élève de l’École polytechnique
- Étudiant de la faculté des sciences de Paris
- Lauréat du concours général
- Éponyme d’un objet céleste
- Famille Poincaré
- Naissance en avril 1854
- Naissance à Nancy
- Décès en juillet 1912
- Décès dans le 5e arrondissement de Paris
- Décès à 58 ans
- Personnalité inhumée au cimetière du Montparnasse (division 16)
- La dernière modification de cette page a été faite le 11 août 2025 à 16:38.

1 729 (nombre de Ramanajan
| 1 729 | |
| Cardinal | mille-sept-cent-vingt-neuf |
|---|---|
| Ordinal | mille sept cent vingt-neuvième 1729e |
| Adverbe | Mille sept cent vingt-neuvièmement |
| Propriétés | |
| Facteurs premiers | 7×13×19 |
| Diviseurs | 7, 13, 19, 91, 133, 247 |
| Autres numérations | |
| Numération romaine | MDCCXXIX |
| Système binaire | 11011000001 |
| Système octal | 3301 |
| Système duodécimal | 1001 |
| Système hexadécimal | 6C1 |
1 729 (mille-sept-cent-vingt-neuf) est l’entier naturel qui suit 1 728 et précède 1 730.
Propriétés
Nombre de Hardy-Ramanujan
1 729 est également connu sous le nom de « nombre de Hardy-Ramanujan » ; il s’agit du plus petit entier naturel s’écrivant de deux manières différentes comme somme de deux cubes :
Il s’agit donc du nombre taxicab d’ordre 2.
Bien qu’elle ait été découverte en 1657 par Bernard Frénicle de Bessy, la propriété de 1 729 ainsi que son nom sont liés à une anecdote relatée par le mathématicien britannique Godfrey Harold Hardy après une visite à son collègue indien hospitalisé Srinivasa Ramanujan, en 1917:
« Je me souviens d’une fois où j’arrivai à son chevet à Putney. J’avais été conduit par le taxi numéro 1 729 ; la morosité qui semblait émaner de ce nombre avait attiré mon attention. J’espérais qu’il ne constituait pas un mauvais présage. “Non, me répondit-il, c’est un nombre fort intéressant ; c’est le plus petit que l’on puisse exprimer comme somme de deux cubes de deux manières différentes.” »
Articles connexes

The Ramanujan Summation:
1 + 2 + 3 + ⋯ ∞ = -1/12
“What on earth are you talking about? There’s no way that’s true!” — My mom !

Mark Dodds
03 Sep 2018
“What on earth are you talking about? There’s no way that’s true!” — My mom
This is what my mom said to me when I told her about this” little” mathematical anomaly. And it is just that, an anomaly. After all, it defies basic logic. How could adding positive numbers equal not only a negative, but a negative fraction? What the frac?
Before I begin: It has been pointed out to me that when I talk about sum’s in this article, it is not in the traditional sense of the word. This is because all the series I deal with naturally do not tend to a specific number, so we talk about a different type of sums, namely Cesàro Summations. For anyone interested in the mathematics, Cesàro summations assign values to some infinite sums that do not converge in the usual sense. “The Cesàro sum is defined as the limit, as n tends to infinity, of the sequence of arithmetic means of the first n partial sums of the series” — Wikipedia. I also want to say that throughout this article I deal with the concept of countable infinity, a different type of infinity that deals with a infinite set of numbers, but one where if given enough time you could count to any number in the set. It allows me to use some of the regular properties of mathematics like commutativity in my equations (which is an axiom I use throughout the article).

For those of you who are unfamiliar with this series, which has come to be known as the Ramanujan Summation after a famous Indian mathematician named Srinivasa Ramanujan, it states that if you add all the natural numbers, that is 1, 2, 3, 4, and so on, all the way to infinity, you will find that it is equal to -1/12. Yup, -0.08333333333.
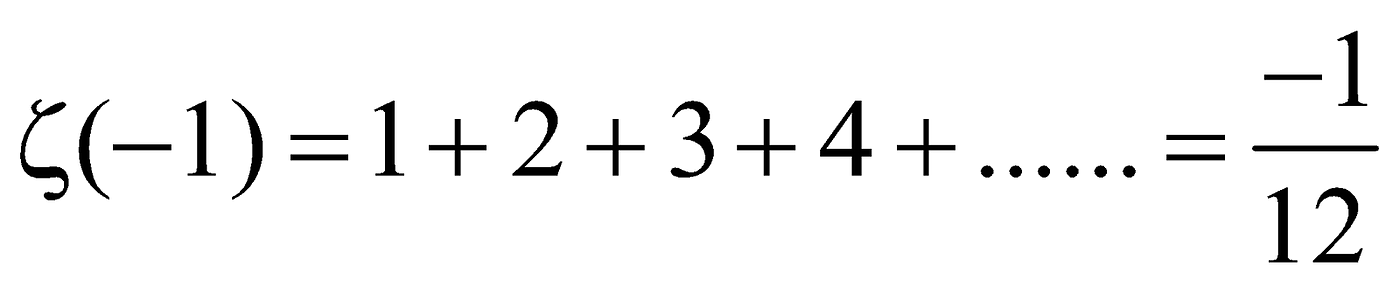
Don’t believe me? Keep reading to find out how I prove this, by proving two equally crazy claims:
- 1–1+1–1+1–1 ⋯ = 1/2
- 1–2+3–4+5–6⋯ = 1/4
First off, the bread and butter. This is where the real magic happens, in fact the other two proofs aren’t possible without this.
I start with a series, A, which is equal to 1–1+1–1+1–1 repeated an infinite number of times. I’ll write it as such:
A = 1–1+1–1+1–1⋯
Then I do a neat little trick. I take away A from 1
1-A=1-(1–1+1–1+1–1⋯)
So far so good? Now here is where the wizardry happens. If I simplify the right side of the equation, I get something very peculiar:
1-A=1–1+1–1+1–1+1⋯
Look familiar? In case you missed it, thats A. Yes, there on that right side of the equation, is the series we started off with. So I can substitute A for that right side, do a bit of high school algebra and boom!
1-A =A
1-A+A=A+A
1 = 2A
1/2 = A
This little beauty is Grandi’s series, called such after the Italian mathematician, philosopher, and priest Guido Grandi. That’s really everything this series has, and while it is my personal favourite, there isn’t a cool history or discovery story behind this. However, it does open the door to proving a lot of interesting things, including a very important equation for quantum mechanics and even string theory. But more on that later. For now, we move onto proving #2: 1–2+3–4+5–6⋯ = 1/4.
We start the same way as above, letting the series B =1–2+3–4+5–6⋯. Then we can start to play around with it. This time, instead of subtracting B from 1, we are going to subtract it from A. Mathematically, we get this:
A-B = (1–1+1–1+1–1⋯) — (1–2+3–4+5–6⋯)
A-B = (1–1+1–1+1–1⋯) — 1+2–3+4–5+6⋯
Then we shuffle the terms around a little bit, and we see another interesting pattern emerge.
A-B = (1–1) + (–1+2) +(1–3) + (–1+4) + (1–5) + (–1+6)⋯
A-B = 0+1–2+3–4+5⋯
Once again, we get the series we started off with, and from before, we know that A = 1/2, so we use some more basic algebra and prove our second mind blowing fact of today.
A-B = B
A = 2B
1/2 = 2B
1/4 = B
And voila! This equation does not have a fancy name, since it has proven by many mathematicians over the years while simultaneously being labeled a paradoxical equation. Nevertheless, it sparked a debate amongst academics at the time, and even helped extend Euler’s research in the Basel Problem and lead towards important mathematical functions like the Riemann Zeta function.
Now for the icing on the cake, the one you’ve been waiting for, the big cheese. Once again we start by letting the series C = 1+2+3+4+5+6⋯, and you may have been able to guess it, we are going to subtract C from B.
B-C = (1–2+3–4+5–6⋯)-(1+2+3+4+5+6⋯)
Because math is still awesome, we are going to rearrange the order of some of the numbers in here so we get something that looks familiar, but probably wont be what you are suspecting.
B-C = (1-2+3-4+5-6⋯)-1-2-3-4-5-6⋯
B-C = (1-1) + (-2-2) + (3-3) + (-4-4) + (5-5) + (-6-6) ⋯
B-C = 0-4+0-8+0-12⋯
B-C = -4-8-12⋯
Not what you were expecting right? Well hold on to your socks, because I have one last trick up my sleeve that is going to make it all worth it. If you notice, all the terms on the right side are multiples of -4, so we can pull out that constant factor, and lo n’ behold, we get what we started with.
B-C = -4(1+2+3)⋯
B-C = -4C
B = -3C
And since we have a value for B=1/4, we simply put that value in and we get our magical result:
1/4 = -3C
1/-12 = C or C = -1/12
Now, why this is important. Well for starters, it is used in string theory. Not the Stephen Hawking version unfortunately, but actually in the original version of string theory (called Bosonic String Theory). Now unfortunately Bosonic string theory has been somewhat outmoded by the current area of interest, called supersymmetric string theory, but the original theory still has its uses in understanding superstrings, which are integral parts of the aforementioned updated string theory.
The Ramanujan Summation also has had a big impact in the area of general physics, specifically in the solution to the phenomenon know as the Casimir Effect. Hendrik Casimir predicted that given two uncharged conductive plates placed in a vacuum, there exists an attractive force between these plates due to the presence of virtual particles bred by quantum fluctuations. In Casimir’s solution, he uses the very sum we just proved to model the amount of energy between the plates. And there is the reason why this value is so important.
So there you have it, the Ramanujan summation, that was discovered in the early 1900’s, which is still making an impact almost 100 years on in many different branches of physics, and can still win a bet against people who are none the wiser.
P.S. If you are still interested and want to read more, here is a conversation with two physicists trying to explain this crazy equation and their views on it’s usefulness and validity. It’s nice and short, and very interesting. https://physicstoday.scitation.org/do/10.1063/PT.5.8029/full/
- My Search for Ramanujan: How I learned to Count* by Ken Ono & Amir D. Aczel
- The Man Who Knew Infinity: A Life of the Genius Ramanujan* by Robert Kanigel
- Ramanujan: Letters and Commentary* by Bruce C. Berndt

e^i.pi=-1
Euler’s identity
From Wikipedia, the free encyclopedia
For other uses, see List of topics named after Leonhard Euler § Identities.
| Part of a series of articles on the |
| mathematical constant e |
|---|
| Properties |
| Natural logarithmExponential function |
| Applications |
| compound interestEuler’s identityEuler’s formulahalf-lives exponential growth and decay |
| Defining e |
| proof that e is irrationalrepresentations of eLindemann–Weierstrass theorem |
| People |
| John NapierLeonhard Euler |
| Related topics |
| Schanuel’s conjecture |
| vte |
In mathematics, Euler’s identity (also known as Euler’s equation) is the equality e^iπ+1=0 (


Euler’s identity is named after the Swiss mathematician Leonhard Euler. It is a special case of Euler’s formula e^ix=cosx+isinx

Mathematical beauty
Euler’s identity is often cited as an example of deep mathematical beauty.[5] Three of the basic arithmetic operations occur exactly once each: addition, multiplication, and exponentiation. The identity also links five fundamental mathematical constants:
- The number 0, the additive identity
- The number 1, the multiplicative identity
- The number π (π = 3.14159…), the fundamental circle constant
- The number e (e = 2.71828…), also known as Euler’s number, which occurs widely in mathematical analysis
- The number i, the imaginary unit such that i2=−1
The equation is often given in the form of an expression set equal to zero, which is common practice in several areas of mathematics.
Stanford University mathematics professor Keith Devlin has said, ”like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler’s equation reaches down into the very depths of existence”. Paul Nahin, a professor emeritus at the University of New Hampshire who wrote a book dedicated to Euler’s formula and its applications in Fourier analysis, said Euler’s identity is ”of exquisite beauty”.
Mathematics writer Constance Reid has said that Euler’s identity is ”the most famous formula in all mathematics”. Benjamin Peirce, a 19th-century American philosopher, mathematician, and professor at Harvard University, after proving Euler’s identity during a lecture, said that it ”is absolutely paradoxical; we cannot understand it, and we don’t know what it means, but we have proved it, and therefore we know it must be the truth”.
A 1990 poll of readers by The Mathematical Intelligencer named Euler’s identity the ”most beautiful theorem in mathematics”.[11] In a 2004 poll of readers by Physics World, Euler’s identity tied with Maxwell’s equations (of electromagnetism) as the ”greatest equation ever”.
At least three books in popular mathematics have been published about Euler’s identity:
- Dr. Euler’s Fabulous Formula: Cures Many Mathematical Ills, by Paul Nahin (2011)
- A Most Elegant Equation: Euler’s formula and the beauty of mathematics, by David Stipp (2017)
- Euler’s Pioneering Equation: The most beautiful theorem in mathematics, by Robin Wilson (2018)
Explanations
Imaginary exponents
Main article: Euler’s formula
See also: Complex exponents with a positive real base

Euler’s identity asserts that eiπ



Euler’s identity therefore states that the limit, as n approaches infinity, of (1+iπn)n

Euler’s identity is a special case of Euler’s formula, which states that for any real number x,eix=cosx+isinx
where the inputs of the trigonometric functions sine and cosine are given in radians.
In particular, when x = π,eiπ=cosπ+isinπ.
Sincecosπ=−1
andsinπ=0,
it follows thateiπ=−1+0i,
which yields Euler’s identity:eiπ+1=0.
Geometric interpretation
Any complex number z=x+iy






Euler’s identity says that −1=eiπ




Additionally, when any complex number z is multiplied by eiθ






Generalizations
Euler’s identity is also a special case of the more general identity that the nth roots of unity, for n > 1, add up to 0:∑k=0n−1e2πikn=0.
Euler’s identity is the case where n = 2.
A similar identity also applies to quaternion exponential: let {i, j, k} be the basis quaternions; then,e13(i±j±k)π+1=0.
More generally, let q be a quaternion with a zero real part and a norm equal to 1; that is, q=ai+bj+ck,

The same formula applies to octonions, with a zero real part and a norm equal to 1. These formulas are a direct generalization of Euler’s identity, since i

History
Euler’s identity is a direct result of Euler’s formula, published in his monumental 1748 work of mathematical analysis, Introductio in analysin infinitorum, but it is questionable whether the particular concept of linking five fundamental constants in a compact form can be attributed to Euler himself, as he may never have expressed it.
Robin Wilson writes:
We’ve seen how [Euler’s identity] can easily be deduced from results of Johann Bernoulli and Roger Cotes, but that neither of them seem to have done so. Even Euler does not seem to have written it down explicitly—and certainly it doesn’t appear in any of his publications—though he must surely have realized that it follows immediately from his identity [i.e. Euler’s formula], eix = cos x + i sin x. Moreover, it seems to be unknown who first stated the result explicitly
See also
Notes
- The term ”Euler’s identity” (or ”Euler identity”) is also used elsewhere to refer to other concepts, including the related general formula eix = cos x + i sin x, and the Euler product formula. See also List of topics named after Leonhard Euler.
References
- Dunham, 1999, p. xxiv.
- Stepanov, S.A. (2001) [1994], ”Euler identity”, Encyclopedia of Mathematics, EMS Press
- Milla, Lorenz (2020), The Transcendence of π and the Squaring of the Circle, arXiv:2003.14035
- Hines, Robert. ”e is transcendental” (PDF). University of Colorado. Archived (PDF) from the original on 2021-06-23.
- Gallagher, James (13 February 2014). ”Mathematics: Why the brain sees maths as beauty”. BBC News Online. Retrieved 26 December 2017.
- Paulos, 1992, p. 117.
- Nahin, 2006, p. 1.
- Nahin, 2006, p. xxxii.
- Reid, chapter e.
- Maor, p. 160, and Kasner & Newman, p. 103–104.
- Wells, 1990.
- Crease, 2004.
- Nahin, Paul (2011). Dr. Euler’s fabulous formula : cures many mathematical ills. Princeton University Press. ISBN 978-0-691-11822-2.
- Stipp, David (2017). A Most Elegant Equation : Euler’s Formula and the Beauty of Mathematics (First ed.). Basic Books. ISBN 978-0-465-09377-9.
- Wilson, Robin (2018). Euler’s pioneering equation : the most beautiful theorem in mathematics. Oxford: Oxford University Press. ISBN 978-0-19-879493-6.
- Conway & Guy, p. 254–255.
- Sandifer, p. 4.
- Wilson, p. 151-152.
Sources
- Conway, John H., and Guy, Richard K. (1996), The Book of Numbers, Springer ISBN 978-0-387-97993-9
- Crease, Robert P. (10 May 2004), ”The greatest equations ever”, Physics World [registration required]
- Dunham, William (1999), Euler: The Master of Us All, Mathematical Association of America ISBN 978-0-88385-328-3
- Euler, Leonhard, Complete work. Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus, Leipzig: B. G. Teubneri
- Kasner, E., and Newman, J. (1940), Mathematics and the Imagination, Simon & Schuster
- Maor, Eli (1998), e: The Story of a number, Princeton University Press ISBN 0-691-05854-7
- Nahin, Paul J. (2006), Dr. Euler’s Fabulous Formula: Cures Many Mathematical Ills, Princeton University Press ISBN 978-0-691-11822-2
- Paulos, John Allen (1992), Beyond Numeracy: An Uncommon Dictionary of Mathematics, Penguin Books ISBN 0-14-014574-5
- Reid, Constance (various editions), From Zero to Infinity, Mathematical Association of America
- Sandifer, C. Edward (2007), Euler’s Greatest Hits, Mathematical Association of America ISBN 978-0-88385-563-8
- Stipp, David (2017), A Most Elegant Equation: Euler’s formula and the beauty of mathematics, Basic Books
- Wells, David (1990). ”Are these the most beautiful?”. The Mathematical Intelligencer. 12 (3): 37–41. doi:10.1007/BF03024015. S2CID 121503263.
- Wilson, Robin (2018), Euler’s Pioneering Equation: The most beautiful theorem in mathematics, Oxford University Press, ISBN 978-0-192-51406-6
- Zeki, S.; Romaya, J. P.; Benincasa, D. M. T.; Atiyah, M. F. (2014), ”The experience of mathematical beauty and its neural correlates”, Frontiers in Human Neuroscience, 8: 68, doi:10.3389/fnhum.2014.00068, PMC 3923150, PMID 24592230
Eternal links
- Exponentials
- Mathematical identities
- E (mathematical constant)
- Theorems in complex analysis
- Leonhard Euler

Les Maths c’est rigolo, mais je préfère mon AMEOUR { Attention Mobilisée et Ouverte dans une Union RADICALE } avec une Femme .
J’ai un mini KODAKPIXPRO FZ45 avec une Aspheric Zoom lens 4x Wide27-108 mm (Equivalent) 1.3.0-6.6 (j’étais obligé d’accepter ce kdo kar j’avais oublié mon Nikon D3600 en déchargeant la Twingo, après avoir raccompagné Soanh et Téo aux Blagis, quel tête en l’air je peux être parfois !

Etonnants classiques : AMOUR ET POéSIE DU MOYEN ÂGE au VIII ième SIèCLE.
De la fin d’Amor à André Chénier.

Jaufré Rudel . Béatrice de Die . Guillaume de Lorris . Alain Chartier . Marie de France . Christine de Pisan Labé . Ronsard . Du Bellay . Marbeuf . Chénier
Ce petit Livre de 157 pages est une Anthologie ( Une anthologie est un recueil de textes ou de morceaux choisis partageant les mêmes caractéristiques : thèmes, genres, styles, langues, origines géographiques, auteurs, etc. Un exemple littéraire ancien est l’Anthologie grecque, un autre musical relativement récent est The Beatles Anthologie) qui présente les poèmes INCONTOURNABLES de la période. Elle entremêle les VOIX de CELLES & CEUX qui,( Christine de pisan) promettent d’aimer d’”Amour SÛRE”.
600 => Terrible belle femme du film ( 600 : Rise of an Empire ) : ARTéMIS, aussi Belle que la Veuve Spartiate de Léonidas.

Horus Dieu à la tête de Faucon, a vengé son Père Osiris en combattant son oncle Seth. Au cours de l’affrontement, l’oeil gauche d’Horus fut arraché, découpé et jeté dans le Nil. Thot, patron des Scribes, parvint à le reconstituer et le rendit à Horus, donnant Naissance à l’oeil Oujdat, un croisement entre un oeil Humain et un oeil de Faucon, qui sert ossi de symbole de mesures égyptiennes.

D’abord, un rappel de Voltes-d’Airs :
” Ô dieu de la Lumière ! Créateur Incréé de la Nature Entière. ”
Le véritable monothéisme, sorti du véritable polythéisme, c’est AHKHéNATON QUI L’A Inventé.
mos ne s’est inspiré que des Livres des Métamorphoses d’Ovide.
terre-promise de mes 2 allez-vous faire EMPALER bande d’usurpateurs hypocrites, menteurs, d’extrême droite hyper fascistes
Comme Poutine et Trump, votre âme est morte à votre naissance …
ATTENTION à la chute !
LES LIMBES VOUS SURVEILLENT d’après les chrétiens
ELLES ATTENDENT SEULEMEMNT LE BON MOMENT POUR VOUS PRéCIPITER DANS LES ENFERS POUR L’éTERNITé !
MASSACREZ, MASSACREZ, C’EST SI FACILE …VOUS N’AVEZ PAS COMPRIS LA HAINE, JUSQU’Où elle est allée celle du barjot d’hitler ! rappelez-vous des cui-cui des fours crématoires
Il y a des MUSULMANS qui disent que les SS ont laissé quelques survivants de la chmolda pour voir de quoi votre secte allait être capable avec l’aide des ricains massacreurs d’INDIENS
Et bien on voit ! Vous-vous acharnez, vous tentez d’exterminer un Peuple
MAIS JAMAIS AU GRAND JAMAIS VOUS NE POURREZ TOUCHER à SON ÂME, comme à celles de tous les autres Indiens LIBRES, vivants ou DCD, Amis de la NATURE
C’est IRRéMéDIABLE.


T.P.I.

Allez, on va au Moyen des Âges (XII ième siècle), kant il y a eu l’invention de l’amour Courtois Epoque des Trouvères, des Troubadours, des Croisés, des Comte qui deviennent ROIS. Comme la ”Licorne” est l’Animal le + important du Bestiaire Fantastique Médiéval, voici ” Je suis comme la Licorne” de Thibaut de Champagne (1201-1253):Mise en scène de 3 allégories
2.Œuvre (peinture, sculpture, film…) dont chaque élément évoque un aspect d’une idée complexe.
1.Narration mettant en œuvre des éléments concrets, chaque élément correspondant à un contenu abstrait.« Le Roman de la Rose » est une longue allégorie de l’amour. )

Si tu fais l’effort de TOUT LIRE de ce metrixleanj.eu qui est maintenant dédié à l’ Amoure Anarchiste
Depuis presque 3 ans, purement du virtuel
c’est allé crescendo cet Amoure a débordé
je le donne à toutes mes AMIES, TOUS leurs petits enfants si rigolos à vouloir tellement vite grandir, je parle aux vents, aux fleurs, je fais des clins-d’oeil aux chats pour les intriguer , Je fais de drôles de sons pour les Corneilles et les Pies, j’attends les Charronnerais qui viennent manger les boules de graines accrochées à la grille de mon salon et quand les écureuils du jardin d’Érasme viennent faire de petits sauts si gracieux.



Je suis comme la Licorne
Troublée de contempler
La Jeune Fille qui l’Enchante,
Si joyeuse de son Supplice,
Que, pâmée, elle Tombe en son Giron,
Et qu’alors on la tue par Trahison.
Moi aussi, m’ont tué, de même Façon,
Amour et ma Dame, oui, c’est vrai :
Ils ont mon coeur que je ne puis reprendre.
Madame, quand devant vous je me trouvai
Et Vous vis pour la première fois,
Mon coeur battait si fort
qu’il resta avec Vous quand je m’en fus

Il fut alors emmené sans rançon,
Prisonnier de la douce geôle
Dont les piliers sont de désir,
Les portes d’agréables visions
Et les chaînes de tendre espoir.
De la Geôle Amour a la clef
Il a placé trois gardiens :
Beau Semblant est le nom du premier,
Beauté en est le maître,
Il a mis refus à l’entrée
Traître répugnant, vif et puant,
Malfaisant et scélérat.
Ces trois là, vifs et hardis,
Ont tôt fait d’attraper un homme.
Qui pourrait souffrir les affronts
Et les attaques de ces portiers
{ tiens, Riders on the Storm vient à mon nesprit ! }
Jamais Roland ni olivier
Ne vainquirent en combattant ;
Mais ceux-là, on les vainc en s’humiliant,
Souffrance porte l’étendard ;
En ce combat dont je vous parle,
Il n’est de Salut que dans la pitié.
Madame, je ne doute rien tant
Que faillir à votre Amour,
J’ai tant appris à souffrir
Que je suis vôtre par habitude.
Dussiez-vous en être fâchée
Je ne puis m’en séparer pour rien au Monde
Sans en garder le souvenir,
Sans que mon coeur soit toujours
En Prison, en étant près de moi.

Oui, tu as raison,
Nous pouvons concevoir Des infinis d’infinis à Une puissance infinie par exemple,
mais nous sommes loin D’être des êtres finis : notre origine matérielle remonte à la nuit des Temps de l’évolution, Nous sommes liés à Toute les formes de vies (du virus au toutou en Passant par la Mitochondrie)
Et dès notre conception Nous recommençons la Fabuleuse histoire du Développement humain Qui ne s’arrête qu’à la fin De notre vie avec tous les souvenirs que nous Laissons derrière nous : Nous devons prendre Conscience de notre éternité, non pas à venir, mais déjà réalisée depuis si longtemps, ce qui permet d’envisager notre fin comme un repos bien mérité,
c’est c’est ça peut être
Le sens de la vie ?
Ecouter ”Au delà du Délire” de Ange.
Nous ne sommes qu’un problème que lorsque nous sommes prisonnier de l’Ego, prisonnier entre les pulsions et les contrôles desquelles il nous faut nous LIBERER
Pour imaginer une nouvelle branche des Mathématiques à partir de TOUS LES SYMBOLES utilisés dans tous les domaines de toutes les SCIENCES.
Mais, pour cela, il faut avoir eu à s’occuper d’enfants ou avoir eu un ou des enfants, pour comprendre à quoi sert la sexualité et comment la dépasser pour dépasser l’Ego puis aller à la recherche du SOI pour terminer dans l’exploration du NOUS : inconscient collectif agissant en PAIX avec nos esprits individuels
Entre l’infiniment petit et l’ensemble vide il y a nécessairement un saut … il faut faire ce saut en cherchant à se dépasser .
1.RYTHME
2.PRESENT
3.PATIENCE
4.FORCE
5.HUMOUR 6.MEDITATION
7. DEPASSEMENT
8. CREATIONS

Mulot de Shrödinberg
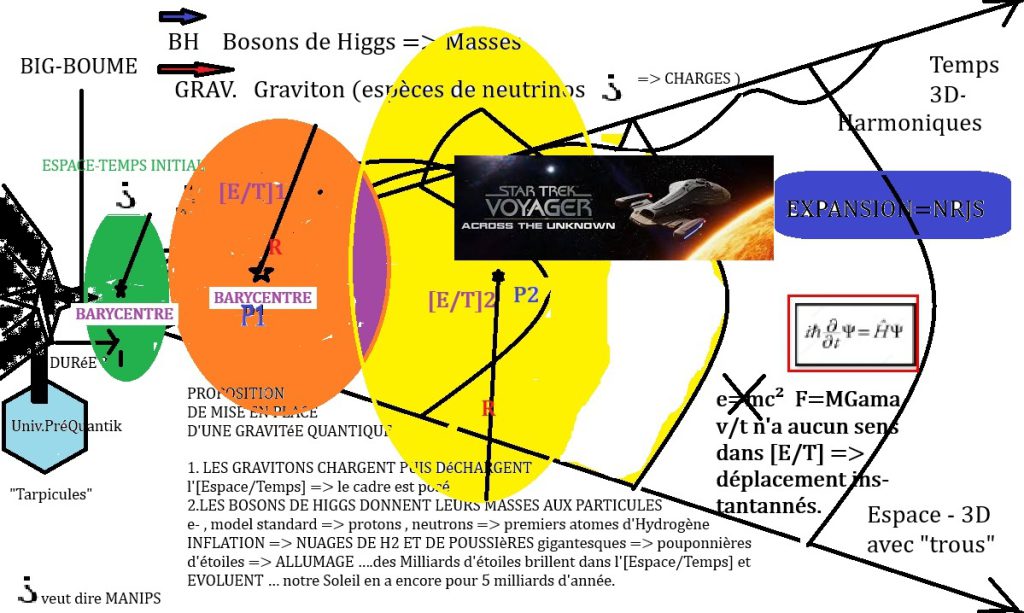
Vision de mise en place de la Gravitation Quantique, l’inflation de l’Univers générant la force qui a été appelée NRJ sombre







CECI EST LA FIN DU MATRIARCAT israélite !






Trump

Gaia





Gaia

A qui faire confiance ?











Un immortel

V pour Vendetta ou comment éliminer les fascistes



Un immortel

Un immortel

Un immortel


Et oui ! Le ”machin” est incapable de faire régner son ordre… tant que certains états se croiront au dessus des lois et ne voudrons pas respecter le Tribunal Pénal InternationalArbre de vie

Lynx ou Caracal


Magie des aurores boréales
Une amie














